Directed Number: addition & subtraction

Using double-sided counters is a great way of helping students to make sense of addition and substraction of negative numbers. I particularly like using MathsBot's double-sided counters as it reduces the difficulties which can sometimes be associated with manipulatives. I tried this out with my year 8s and really found that they were able to make sense of calculation of negative numbers in a way that previous classes haven't been able to. 

Representing values

I spent lots of time getting them used to representing values with double-sided counters. The idea is that one side is positive and the other side is negative, and a positive counter cancels out a negative counter. The representations below are therefore all equivalent.

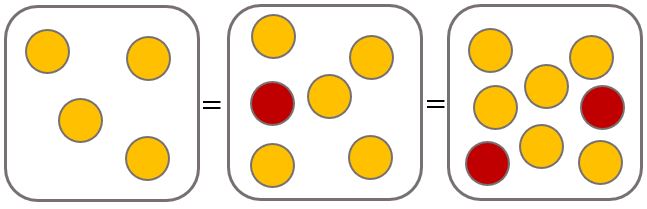
I also spent a little bit of time right at the start to ensure they were secure with vertical number lines. I don't remember where I first saw this idea but essentially you give them 0 and one marking either side, and then another point to label (horizonal number line below for space).

Having previously been fairly ambivalent about the use of minus and negative, I decided that, having a something fairly tangible representing a negative, it was important to distinguish between negative as an adjective and subtract as a verb. "Minus" in the sense of \(5-3=2\) is supposedly a preposition which felt more confusing: subtracting was doing something physical with the counters so using a verb felt more appropriate. I didn't ban the word minus but I did explain that in everyday language minus is used to to mean both negative and subtract, and I did spend some time working on mini-whiteboards asking whether it was a negative sign or a subtraction sign. For example, what's the role of the \(-\) in this calculation: \(-4+3\)? And this one: \(4-3\)? I decided not to use an alternative notation (for example \(^{-}3\) or \((-3)\) in brackets) as I don't think this is something you see outside of the context of maths classrooms.

Another point which I emphasised was that a negative number can be thought of as the opposite of a positive number i.e. \(-3\) is the opposite of \(3\). The vertical number lines were useful here as we could discuss a line of symmetry at zero. This was less useful for addition and subtraction but was useful when thinking about multiplying two negatives together.

Generalising addition

Once students were secure with representing negative numbers, we then spent some time on generalising what happens when you add a positive number, and what happens when you add a negative number. Breaking it down into the different cases is also helpful, i.e. what happens when you add a positive to a positive, what happens when you add a positive to a negative, what happens when you add a positive to some arbitrary number \(n\)? You can then do similar for adding negatives. Drawing students' attention to this explicitly feels important as we don't want students to need the counters indefinitely. Again, the use of the vertical number line was useful here as you can see that, when you add a positive number, the value increases (moves up the number line) and when you add a negative number it decreases (moves down the number line).  Before moving onto subtraction, students worked on various addition questions. Don Steward has some excellent directed number arithmogons and I also like this Venn diagram activity from Craig Barton's Maths Venns website.

Zero pairs

Taking away something which isn't there requires thought! For example, using double-sided counters to represent \(-5-2\) or \(5--2\) is more difficult than \(5-2\) where you can just remove two positive counters or \(-5--2\) where you can just remove two negative counters. This is where the time spent on representing values pays off. To take the first example, you can represent \(-5\) with seven negative counters and two positive counters, essentially adding in two positive counters and two negative counters. You can then remove the two postive counters leaving you with seven negative counters, i.e. \(-5-2=-7+2-2=-7\). Adding in zero pairs like this is also useful as a precursor to using zero pairs with algebra tiles.

Generalising subtraction

After some discussion around zero pairs, we then spent time generalising subtracting negatives in a similar way to addition. So, trying to generalise what happens when you subtract a positive from a positive, what happens when you subtract a positive from a negative, what happens when you subtract a positive from some arbitrary number \(n\)? Considering the cases again has the advantage of making it more persuasive for students. You can then do similar for subtracting negatives, perhaps noting that subtracting a positive is equivalent to adding a negative in that the value decreases, and subtracting a negative is equivalent to adding a positive in that the value increases. Following this, students completed various tasks on addition and subtraction with negative numbers. In particular, NRICH's lovely Weights tasks gives students lots of practice on negative numbers, plus some nice order of operations questions from Don Steward and some magic squares from MathsPad.

Resources

My sequence of lessons (which includes the resources named above, plus these questions from Increasingly Difficult Questions can be found here. Let me know what you think! Tweet to @jamesbakermaths.